Published: Dec 27, 2020 by Dev-hwon
이 내용은 고려대학교 강필성 교수님의 Business Analytics 수업을 보고 정리한 것입니다.
아래 이미지 클릭 시 강의 영상 Youtube URL로 넘어갑니다.
Genetic Algorithm
-
시행 착오를 효율적으로 수행하여 복잡한 문제 해결
-
자연 시스템의 작동 방식을 모방
-
생물의 재생산을 모방한 진화 알고리즘
-
재생산 과정을 반복하여 우수한 솔루션을 찾고 보존
| 단계 | 설명 |
|---|---|
| Selection | 품질 향상을 위한 우수한 솔루션 선택 |
| Crossover | 현재 솔루션을 기반으로 다양한 대안 검색 |
| Mutation | 지역 옵티마에서 벗어날 수 있는 기회를 준다 |
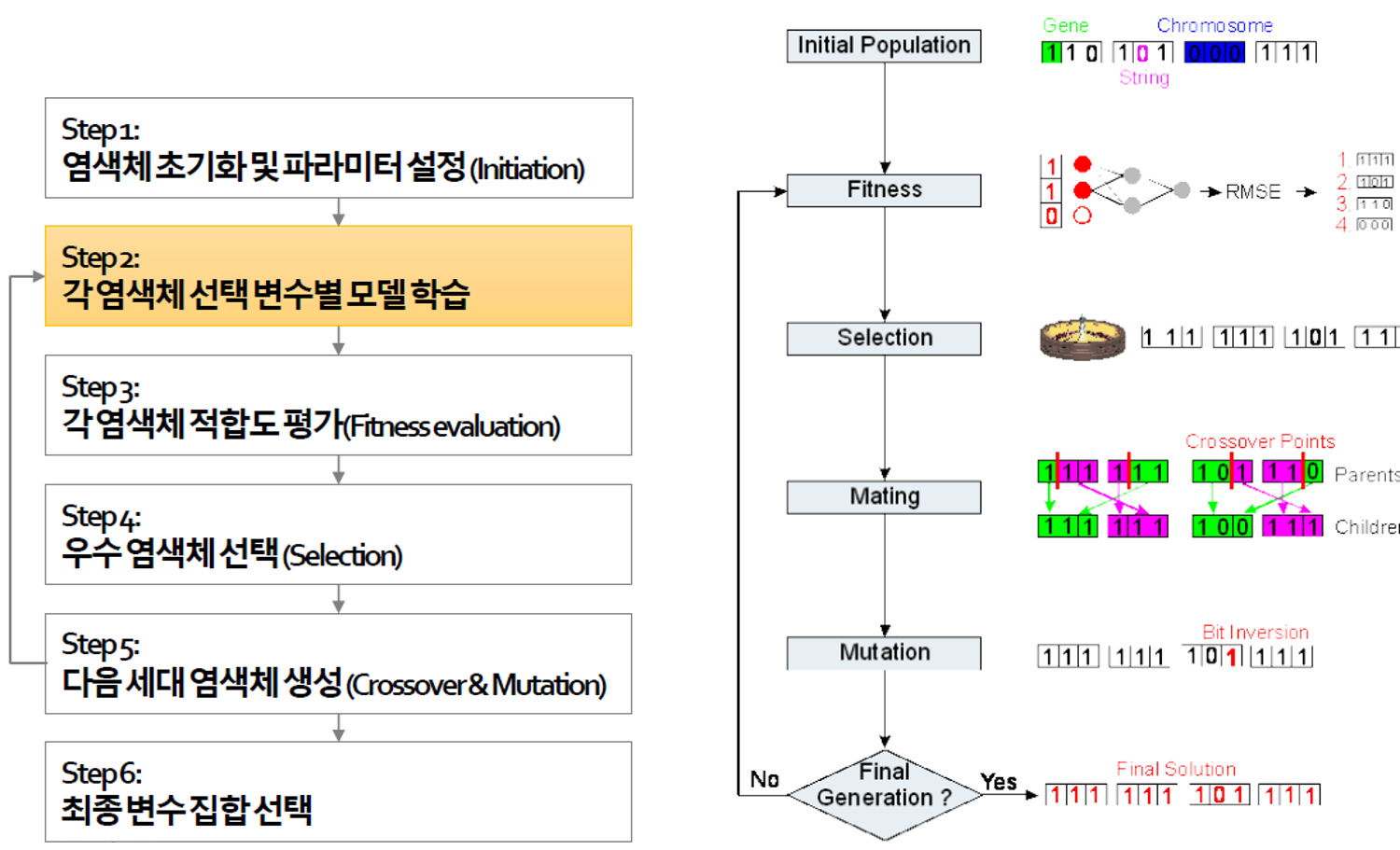
GA Step 1: Initialization
Encoding Chromosomes
-
변수 선택뿐만 아니라 광범위한 최적화 문제에 사용할 수 있다.
-
목적에 따라 Encoding schme 자체가 달라진다.
-
Binary encoding을 주로 사용한다.

Parameter Initialization
- The number of chromosome (population)
- Fitness function -> chromosome quality 평가 함수
- Crossover mechanism
- The rate of mutation
- Stopping criteria
- minimum fitness improvement
- maximum iterations, etc.
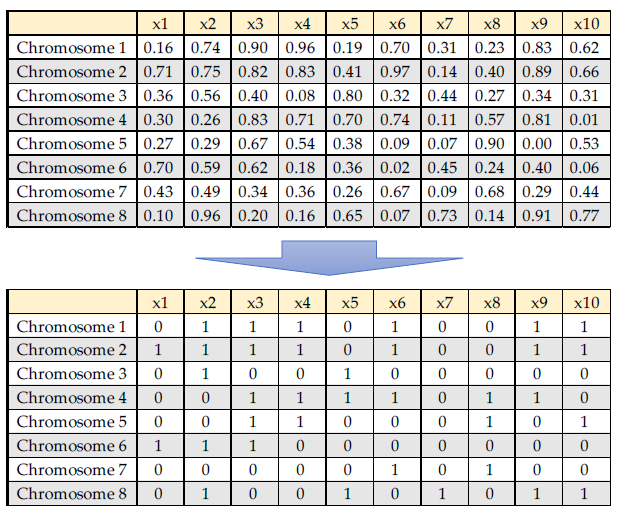
Example: Population Initialization
- 각 gene에 대한 난수 생성
- 난수를 이진 값으로 변환 (이 예에서는 cut-off = 0.5)
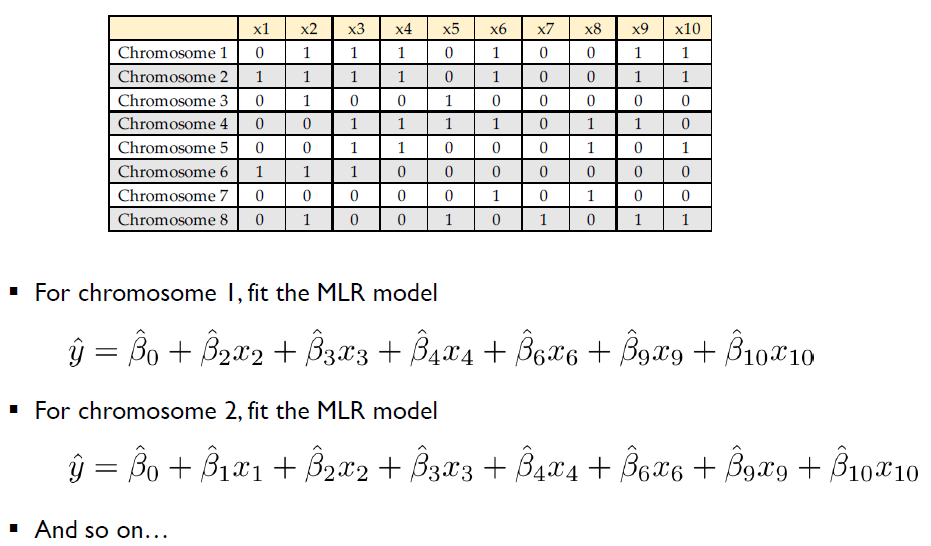
Example: Train the model
- 모델이 다변량 선형 회귀 (MLR)라고 가정
GA Step 2: Fitness Evaluation
Fitness Function
- 다른 gene보다 더 나은 gene를 결정하는 기준
- 일반적으로 fitness value가 높을수록 chromosome이 더 좋다.
- fitness function에 포함된 공통 기준
- 두 gene의 fitness value가 같으면 변수가 적은 gene 선호
- 두 gene이 동일한 수의 변수를 사용하는 경우 예측 성능이 더 높은 것을 선호
Example: Fitness Function
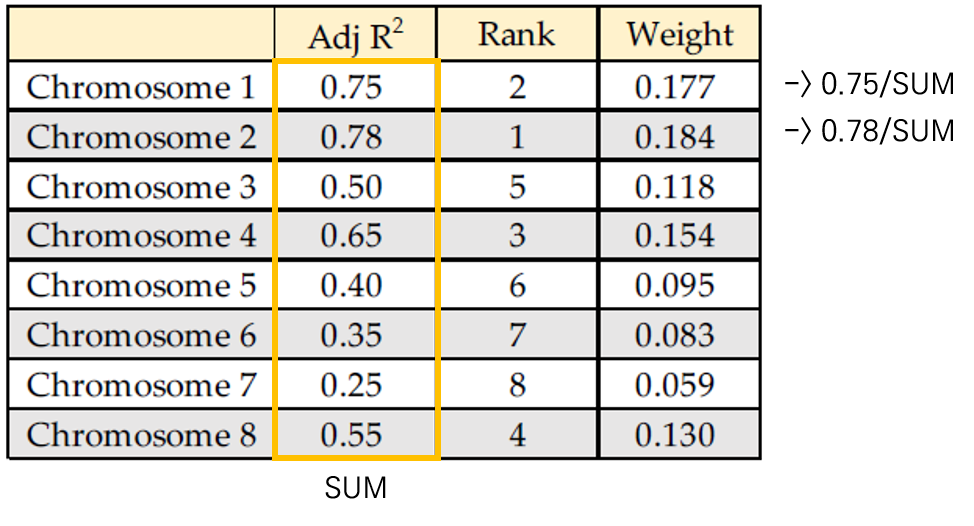
GA Step 3: Selection
- 현재 population에서 우수한 gene을 선택하여 차세대 population을 재현
- Determicistic Selection
- Gene의 상위 N%만 선택
- 하단 (100-N)% gene은 선택되지 않는다.
- Probabilistic Selection
- 각 gene의 적합성 값을 선택 가중치로 사용
- 모든 gene은 다른 확률로 선택 될 수 있다.
Example: Selection
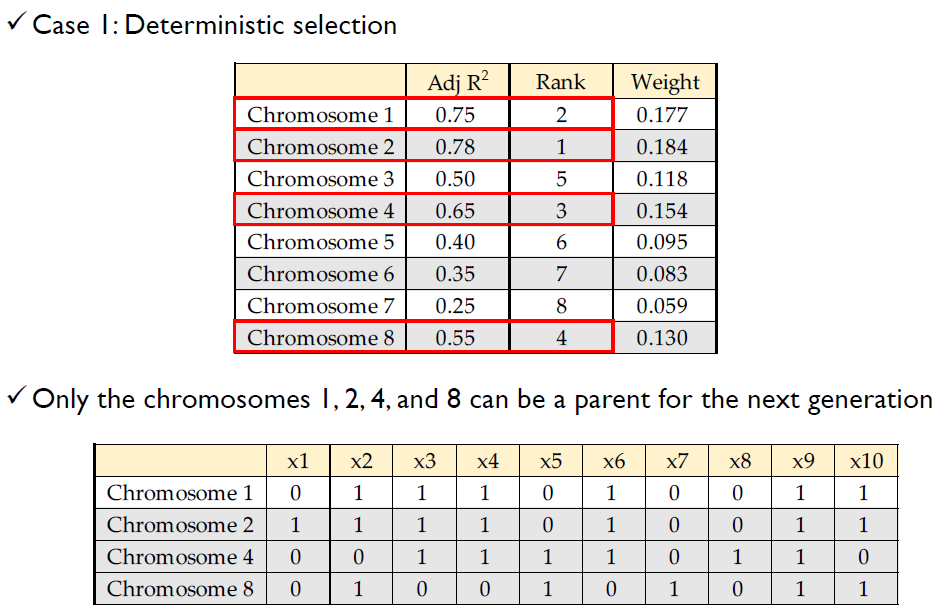
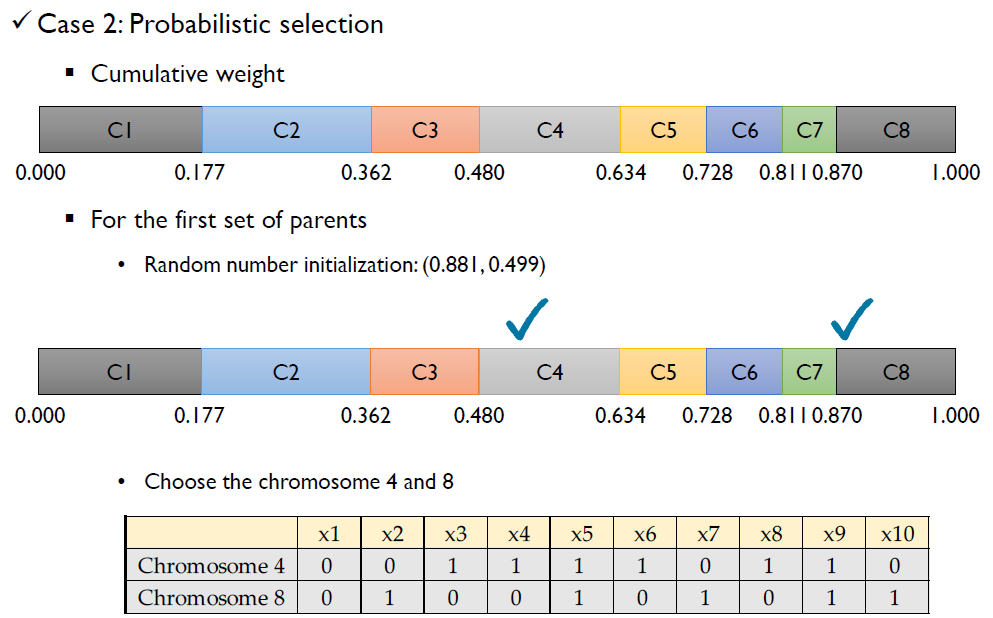
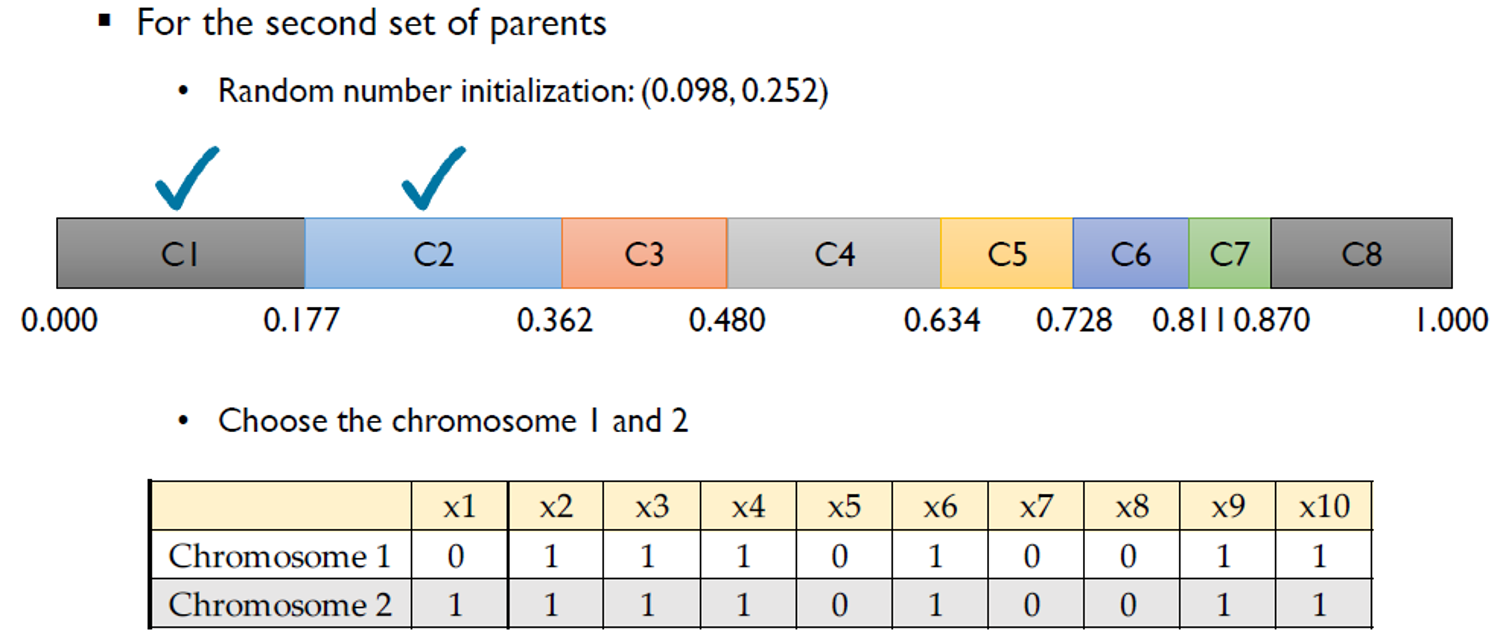
GA Step 4: Crossover & Mutation
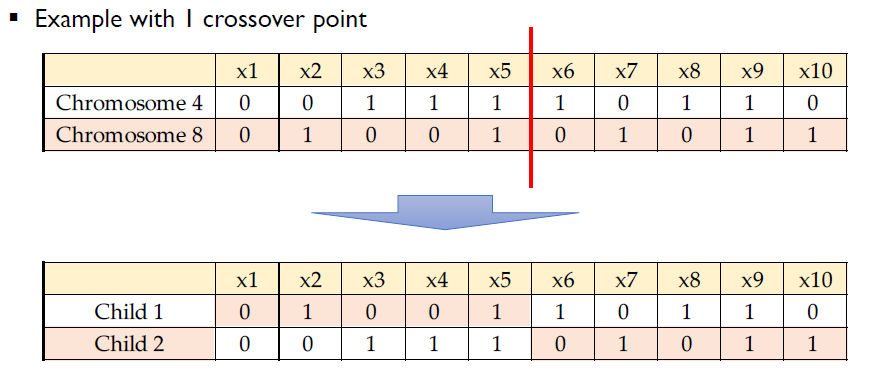
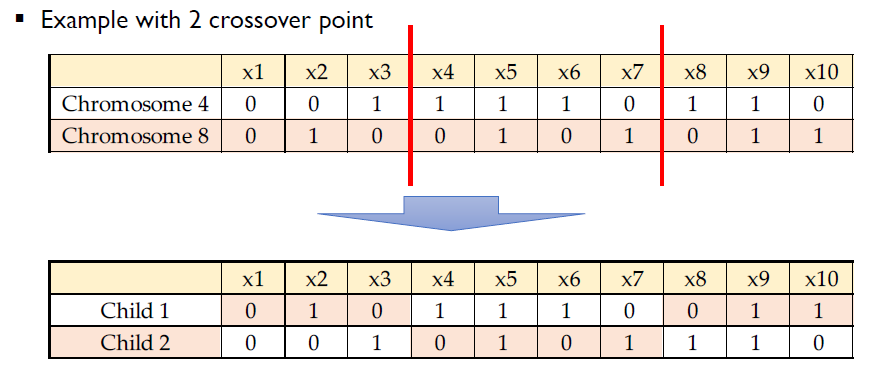
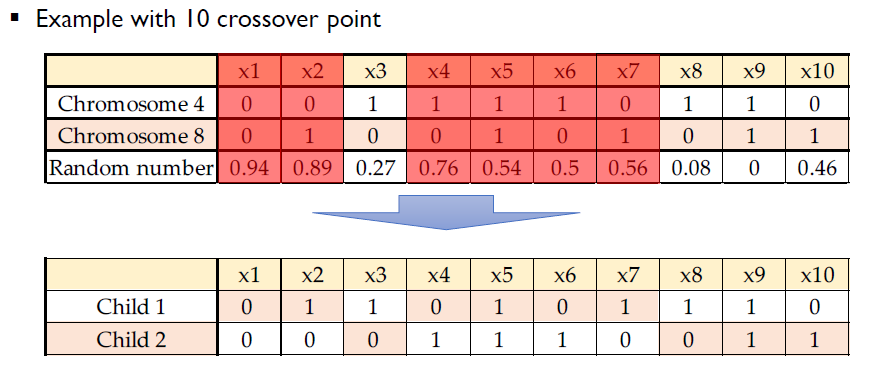
Crossover
- 두 개의 child chromosomes는 두 개의 parent chromosome에서 생성된다.
- Crossover 수는 1에서 n (총 gene 수)까지 다양 할 수 있다.
Mutation
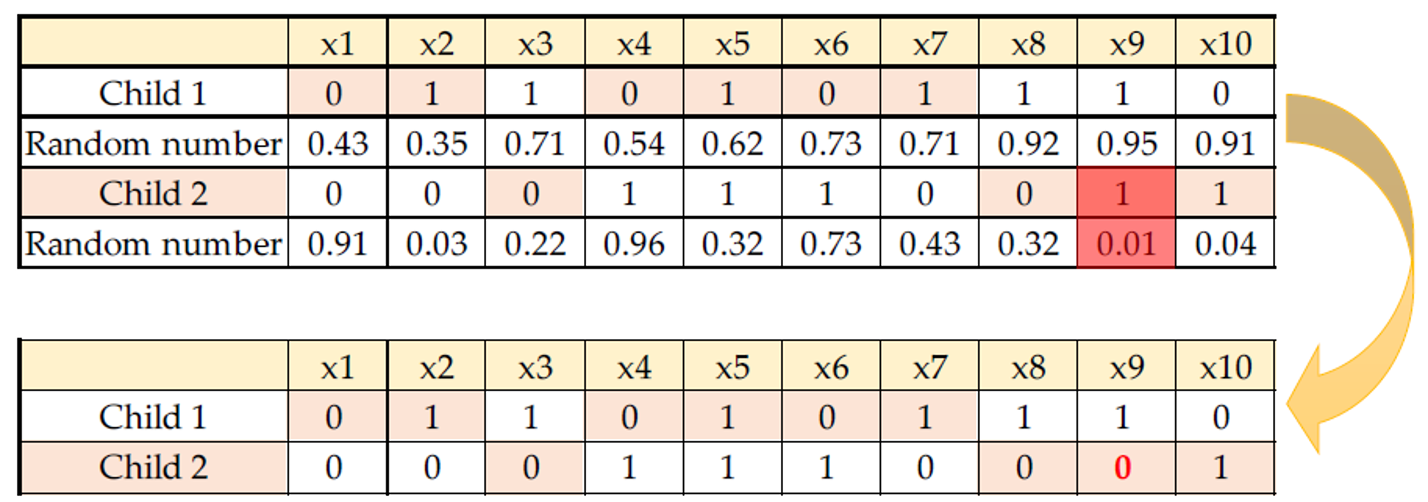
- 한 세대의 chromosome 집단에서 다음 세대까지 다양성을 유지하는 데 사용되는 유전 연산자
- chromosome의 초기 상태에서 하나 이상의 gene value를 변경하여 완전히 새로운 gene value가 gene pool에 추가
- 변이를 통해 현재 솔루션은 로컬 옵티마에서 벗어날 수 있다.
- 너무 많은 돌연변이율은 수렴 시간을 증가시킬 수 있다 (0.01이 좋은 선택 일 수 있음)
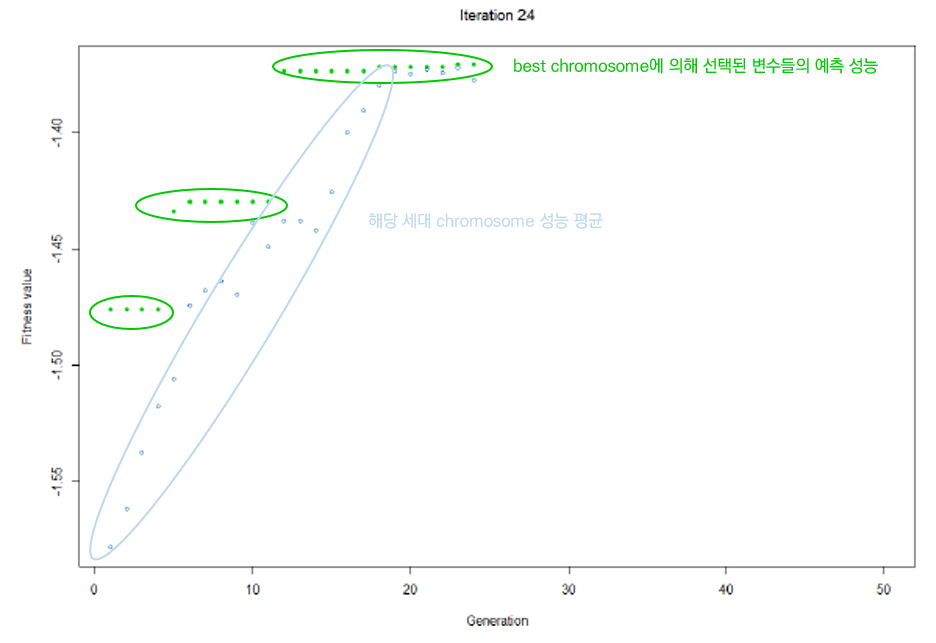
GA Step 5: Find the Best Solution
- 최적의 변수 부분 집합 찾기
- 중지 기준을 충족한 후 fitness value가 가장 높은 gene을 선택한다.
- 일반적으로 초기 단계에서 상당한 fitness 향상이 발생하며, 이는 몇 세대 후에 미미하게 된다.
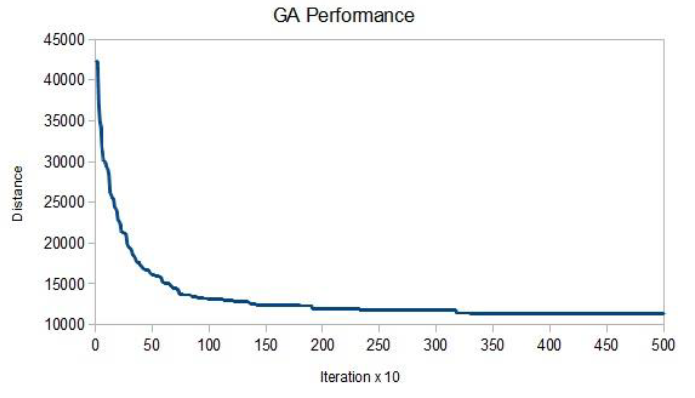
Empirical Study
- Rankings in terms of
- Error rate improvement
- Variable reduction rate
- Computational efficiency
| Variable selection technique | Error rate improvement | Variable reduction rate | Computational efficiency |
|---|---|---|---|
| Forward | 5 | 4 | 1 |
| Backward | 4 | 3 | 2 |
| Stepwise | 3 | 2 | 6 |
| GA | 1 | 6 | 7 |
| Ridge | 2 | 7 | 5 |
| Lasso | 7 | 1 | 3 |
| Enet | 6 | 5 | 4 |



